One approach to solving the problem is to map the times 00:00 to 23:59 to a circle and then compute the chord length between the two mappings. For a discussion on how to compute chord length, please refer to the Wikipedia article "Circular Segment."
Below is a picture of a circle with the cord length denoted by c
The general equation to compute the length of the chord is given by the equation below

For simplicity will pick R to be 1. The above equation now simplifies to the following

The above concepts and math was implemented in the following code using Python 3.6.
import math
def create_hours_minutes_in_a_day():
number_of_hours_in_day = 24
number_of_minutes_in_an_hour = 60
number_of_minutes_in_a_day = 0
hours_minutes_in_day = []
for hour in range(0, number_of_hours_in_day):
if hour < 10:
hour_to_print = '0' + str(hour)
else:
hour_to_print = str(hour)
for minute in range(0, number_of_minutes_in_an_hour):
if minute < 10:
minute_to_print = '0' + str(minute)
else:
minute_to_print = str(minute)
hours_minutes_in_day.append(hour_to_print+':'+minute_to_print)
number_of_minutes_in_a_day += 1
return hours_minutes_in_day, number_of_minutes_in_a_day
def map_hour_minute_in_day_to_circle(hour_colon_minute_in_day, number_of_minutes):
number_of_degrees_in_a_circle = 360
increment_size_in_degrees = number_of_degrees_in_a_circle / number_of_minutes
current_angle_in_degrees = 0
map_hour_minute_to_circle = dict()
for x in hour_colon_minute_in_day:
map_hour_minute_to_circle[x] = current_angle_in_degrees
current_angle_in_degrees += increment_size_in_degrees
return map_hour_minute_to_circle
def compute_arc_length_between_time_interval(mapping_of_hour_minute_to_angle, time_a, time_b):
# Since we want the relative distance betwee two time intervals,
# can set the circle to a radius = 1
angle_a = mapping_of_hour_minute_to_angle[time_a]
angle_b = mapping_of_hour_minute_to_angle[time_b]
chord_length = 2 * math.sin ( math.radians(angle_b - angle_a) / 2 )
print("Time A: ", time_a, "Angle A: ", angle_a)
print("Time b: ", time_b, "Angle A: ", angle_b)
print("Chord: ", chord_length)
print("---")
hour_colon_minute_in_day, number_of_minutes = create_hours_minutes_in_a_day()
map_hour_minute_to_angle = map_hour_minute_in_day_to_circle(hour_colon_minute_in_day, number_of_minutes)
compute_arc_length_between_time_interval(map_hour_minute_to_angle, '00:00', '06:00')
compute_arc_length_between_time_interval(map_hour_minute_to_angle, '00:00', '12:00')
compute_arc_length_between_time_interval(map_hour_minute_to_angle, '00:00', '18:00')
compute_arc_length_between_time_interval(map_hour_minute_to_angle, '00:00', '23:59')
The output from the above code is below
Time A: 00:00 Angle A: 0 Time b: 06:00 Angle A: 90.0 Chord: 1.4142135623730951 --- Time A: 00:00 Angle A: 0 Time b: 12:00 Angle A: 180.0 Chord: 2.0 --- Time A: 00:00 Angle A: 0 Time b: 18:00 Angle A: 270.0 Chord: 1.4142135623730951 --- Time A: 00:00 Angle A: 0 Time b: 23:59 Angle A: 359.75 Chord: 0.0043633196686735124 ---



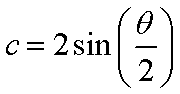
Article: Top 6 errors novice machine learning engineers make by Christopher Dossman - Oct 15, 2017
ReplyDeletehttps://medium.com/towards-data-science/top-6-errors-novice-machine-learning-engineers-make-e82273d394db
Not properly dealing with cyclical features
Hours of the day, days of the week, months in a year, and wind direction are all examples of features that are cyclical. Many new machine learning engineers don’t think to convert these features into a representation that can preserve information such as hour 23 and hour 0 being close to each other and not far.
Keeping with the hour example, the best way to handle this is to calculate the sin and cos component so that you represent your cyclical feature as (x,y) coordinates of a circle. In this representation hour, 23 and hour 0 are right next to each other numerically, just as they should be.
Take Away: If you have cyclical features and you are not converting them you are giving your model garbage data to start with.